◆[招考公告]公务员信息汇总	◆[qq群]贵州公务员交流群： 461734862
	◆[笔试培训]公务员招考笔试培训	◆[视频]公务员招考视频备考资料
	◆[面试培训]公务员招考面试培训	◆[微信] 新文泰微信客服咨询号：xwtjy_01
	◆[备考资料]公务员招考备考资料	◆[电话]咨询电话：0851 —86785360

若a，b是实数，则，等号当且仅当a=b的时候取得。

【解析】设应降低x元，总利润为y元，则降低后的销售单价为（100-x）元，销量为（120+20x）件，进货单价为80元，则总利润y=（100-x-80）×（120+20x），将其化简成函数式为，根据一元二次函数图像性质，当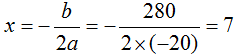时，y最大。故本题选C。

【解析】设提高x档，则每件产品的利润增加2x元，日产量减少5x件，总利润为y元，每天获得的利润为y=（8+2x）×（60-5x）=10×（4+x）×（12-x）元，因为（4+x）+（12-x）=16是定值，根据均值不等式原理，故当且仅当4+x=12-x时，即x=4时，（4+x）×（12-x）的值最大，即可获得最大利润，为10×（4+4）×（12-4）=640元。故本题选C。

公务员、事业单位、教师招考笔试/面试培训课程